In this post I've included some comparisons with the EJML library. I've included these as EJML provides the best performing single-threaded, non-native matrix implementation for small to medium sized matrices I know of. Note that I've used the simplest way of performing the operations in EJML, as I am attempting to highlight design/performance aspects of Thorwin Math matrices, not making a balanced performance comparison.
Matrix Operations Performance
Lets first take a look at the performance characteristics of the addition of two matrices. First, we take a look at small matrices. The following graph shows the performance for A(d,d) + B(d,d) and A(d,d) + B'(d,d).At dimensions in access of 5x5 this advantage is lost. At this point Thorwin Math will use a regular packaged array based implementation, which results in performance that is comparable to EJML.
Adding a transposed matrix for very small (up to and including 5x5) matrices performs really well, as transposing is completely generated and consists of creating a new instance of an object.
At dimensions in access of 5x5, the packed array implementation is used. As the packed array implementation supports both row-major and column-major, it can perform the addition and transposing in a single pass. This results in better performance than performing a transpose on the data, followed by an addition.
The following chart shows the performance of the addition for larger matrix dimensions.
For larger matrices, the addition is implemented using multiple threads. There is a speed-up compared to the single-threaded EJML baseline. It does not, however, scale up to the number of cores (in this case 4), as it bound by memory speed.
The following charts shows multiplication of (square) matrices at various dimensions. We start with small matrix dimensions.
The generated matrices up to and including 5x5 show a definite performance advantage over the packed array implementation. From dimensions of 6 and up the advantage is gone and the performance is on-par with EJML. The Thorwin Math implementation shows a slight performance advantage. I think this is just due to the fact that Thorwin Math operates directly on the packed array, where EJML's SimpleMatrix uses an extra layer of indirection.
The followng chart shows medium to large matrices. This chart includes the performance of Thorwin Math using the accelerator (Thorwin Math Accelerator).
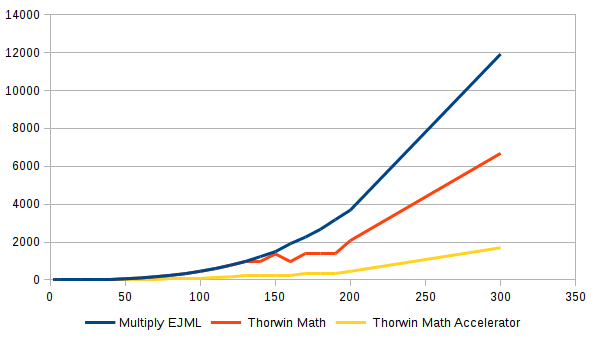
Thorwin Math and EJML stay on-par up to the moment Thorwin Math switches to the block matrix implementation. From this point Thorwin Math starts to use multiple threads. From dimensions around 150 the performance seems to wobble somewhat. This is likely because of the block size or 32x32. As matrix dimensions are not multiples of 32, padding is added. This padding takes part in the multiplication, slowing down when there is relatively large amounts of padding. This is the case around dimensions of 150. At 160 (5*32), speed is optimal again. At higher dimensions, the padding is relatively insignificant, so the wobble is not visible.
What is very clear in this chart is that native, optimized code is a lot faster than the regular Java code.
This last chart shows multiplication performance for larger matrices. This shows that even at these dimensions, native optimized code outperforms the Java code by a factor of about 2, which is a lot less than at dimensions below 1000.
At dimension of 5000x5000 the multi-threaded Thorwin Math multiplication seems to be almost 4 times as fast as the single-threaded EJML baseline. It seems the algorithm scales well for the number of cores in use.